LE MODELE QUANTIQUE DE L'ATOME
QUELQUES NOTIONS DE MECANIQUE QUANTIQUE
Le modèle simple de l'atome que nous avons utilisé jusqu'ici est basé sur le modèle de Bohr, lui-même basé sur la mécanique classique. Ce modèle classique ne permet pas de décrire correctement le comportement des atomes ou des molécules. Le début de ce siècle a vu la naissance d'une nouvelle mécanique adaptée à ces objets minuscules. Cette nouvelle mécanique à reçut le nom de mécanique ondulatoire ou de mécanique quantique. Nous allons dans ce chapitre en décrire les rudiments.
Dualité onde - corpuscule - Ondes de De Broglie :
La lumière possède apparemment une double nature à la fois ondulatoire et corpusculaire.
L'aspect ondulatoire se manifeste lors de tous les phénomènes relevant de l'optique classique (réflexion et réfraction et diffraction). A la fin du IXX° siècle on considérait la lumière comme purement ondulatoire. Au début du XX° siècle, l'étude de nouveau phénomènes, tel que le rayonnement du corps noir (Planck 1900) ou l'effet photoélectrique (Einstein 1905) conduisent à reconsidérer la nature de la lumière et à lui redonner le statut corpusculaire que Newton lui avait attribué originellement. Selon cette théorie la lumière est composée de particules appelées photons et transporte une énergie proportionnelle à sa fréquence : E = h n. (h est la constante de Planck). Notons que cette théorie corpusculaire contient tout de même une fréquence de nature ondulatoire. Ces deux aspects ne s'opposent pas et sont complémentaires l'un de l'autre.
D'un autre coté, le modèle de Bohr traitant de l'atome en tant que pure particule fait intervenir une quantification qui fait apparaître des nombres entiers, or les nombres entiers interviennent naturellement dans l'étude des phénomènes de diffraction typiquement ondulatoires. En 1924, Louis de Broglie généralisa cette dualité onde - corpuscule à toute la matière en postulant qu'à toute particule de matière en mouvement était associée une onde dont la fréquence est reliée à la quantité de mouvement p selon la relation : l = h / p ou l = h / m v.
Voyons comment de Broglie pu établir cette formule :
N'oublions pas qu'une nouvelle théorie vient de révolutionner la physique, c'est la théorie de la relativité d'Einstein.
Cette théorie fait entre autre correspondre masse et énergie par la célèbre formule E = m C2.
Le photon doit satisfaire les deux égalités simultanément : E = m C2 et E = h n
m C2 = h n = h C / l
d'où l = h C / m C2
l = h / m C = h / p
A l'échelle macroscopique, celle des objets courants, cette onde ne peut se manifester et est totalement inobservable (voir T.D), mais pour les particules minuscules du monde des atomes cet aspect ondulatoire est réel comme l'ont montré en 1927 Davisson et Germer en faisant diffracter comme une onde un faisceau d'électrons.
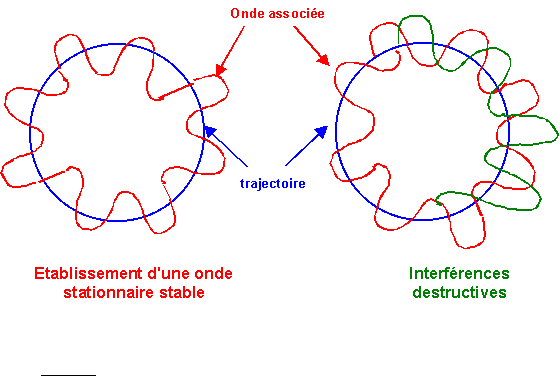
L'utilisation de ces ondes de De Broglie permet par exemple de retrouver la condition de quantification utilisée par Bohr. L'électron en tournant sur son orbite circulaire est "accompagné" de son onde de De Broglie qui tourne avec lui. Pour que l'onde puisse être stationnaire il faut qu'elle n'interfère pas avec elle-même (soit en phase avec elle-même). Cette condition n'est remplie que si la longueur de la trajectoire contient exactement un nombre entier de fois la longueur d'onde.
Soit 2 p R = n l = n (h / p) = n (h / m v )
soit finalement : m v R = n ( h / 2 p)
On retrouve la condition de quantification du moment cinétique postulée par Bohr, mais elle trouve ici une explication rationnelle.

L'équation de Schrödinger
On peut donc associer une onde Y a l'électron de l'atome d'hydrogène, cette onde sera décrite par une fonction mathématique appelée fonction d'onde (ou parfois orbitale).
En 1926, Schrödinger établit une équation différentielle permettant de calculer à priori ces fonctions d'ondes.
{(¶ 2 Y / ¶ x2) + (¶ 2 Y / ¶ y2) + (¶ 2 Y / ¶ z2) } + (8 p2 m / h2) ( E - V ) Y = 0
x, y et z sont les coordonnées cartésiennes de l'électron dans un repère lié au noyau.
m est la masse de l'électron
h est la constante de Planck
E est l'énergie totale de l'électron et V son énergie potentielle.
Cette équation de Schrödinger constitue le fondement de la mécanique quantique.
La résolution d'une telle équation différentielle est très ardue et ne sera pas abordée ici. Dans le cas de problèmes à un seul électron comme l'atome d'Hydrogène ou les Hydrogénoïdes on peut la résoudre sans approximations et la résolution permet de retrouver l'expression de l'énergie établie dans le modèle de Bohr : E = - ( m e4 / 8 e2 h2 ) ( 1 / n2 )
La résolution amène de plus naturellement les 3 nombres quantiques n, l, et m ainsi que les relations entre eux.
Pour les systèmes à plus d'un électron la résolution est impossible sans avoir recours à des approximations.
Signification physique de la fonction d'onde :
La fonction d'onde par elle-même n'a pas de signification physique, en revanche la valeur de son carré en un point de l'espace détermine la probabilité de présence de l'électron dans un volume dV autour de ce point.
dP = Y 2 dV
Le rapport dP/dV = Y 2 est appelé densité de probabilité de présence de l'électron au point considéré.
L'inégalité d'Eisenberg (ou principe d'incertitude) :
Cet aspect probabiliste est confirmé par l'inégalité d'Heisenberg énoncée en 1927. Ce principe affirme qu'on ne peut connaître simultanément la quantité de mouvement d'une particule et sa position. Si on appelle Dx l'incertitude sur la position et Dp l'incertitude sur la quantité de mouvement alors l'inégalité suivante sera vérifiée : Dx Dp > h / 2 p
Cette inégalité peut aussi s'écrire Dx Dv > h / ( 2 p m) (en remplaçant Dp par m Dv).
Il ne s'agit pas la d'une imprécision des mesures expérimentales mais bien d'un principe fondamental de nature théorique. On peut mesurer exactement ces deux grandeurs x et v indépendamment et séparément l'une de l'autre mais on ne pourra connaître que l'une de ces deux grandeurs avec une précision arbitrairement fixée plus cette précision sera grande et plus l'incertitude sera grande sur l'autre grandeur. En pratique, h = 6,63 10-34 Js et le rapport h/2p est pratiquement égal à 10-34 on a donc Dx DV > 10-34 / m pour des objets de masse ordinaire ( 1g ,1 Kg ou 1 t) le produit des incertitudes est donc très petit et on connaît donc à la fois x et v avec une grande précision. Dans le cas d'un véhicule de 1 tonne DX DV = 10-37 , si l'on suppose connue la position du véhicule à 1 m prés l'incertitude sur sa vitesse sera de 10-37 m/s. Soit une précision extraordinaire, on ne pourra donc invoquer le principe d'incertitude pour contester une contravention pour excès de vitesse. Comme les ondes de De Broglie ce principe n'a aucune incidence sur les objets macroscopique et ne devient important que si l'on s'intéresse à des particules de masse très faible. Pour un électron de masse 10-30 kg le produit Dx Dv = 10-4 , si l'on suppose sa vitesse connue au m/s près ce qui est une mauvaise précision, sa position sera connue à 10-4 m près ce qui est gigantesque par rapport à la taille des atomes (10-10m).
La mécanique quantique nous oblige à renoncer à une vision classique de l'univers. Des notions telle que celle de trajectoire d'une particule n'ont plus de signification dans cette théorie. Le comportement des objets quantiques est régit par des lois probabilistes et le déterminisme auquel la physique classique nous a habitués doivent être abandonné ce qui heurte parfois le bon sens commun…
Résultats pour l'atome d'Hydrogène :
Nous allons présenter succinctement et sans entrer dans les détails mathématiques les principaux résultats obtenus par la mécanique quantique dans le problème le plus simple qu'elle puisse traiter, celui de l'atome d'hydrogène ne comportant que deux particules (un proton et un électron). Pour simplifier le problème, le proton beaucoup plus massif que l'électron sera supposé fixe. La symétrie du problème est sphérique, on utilisera donc les coordonnées sphériques plutôt que les coordonnées cartésiennes pour résoudre l'équation de Schrödinger.
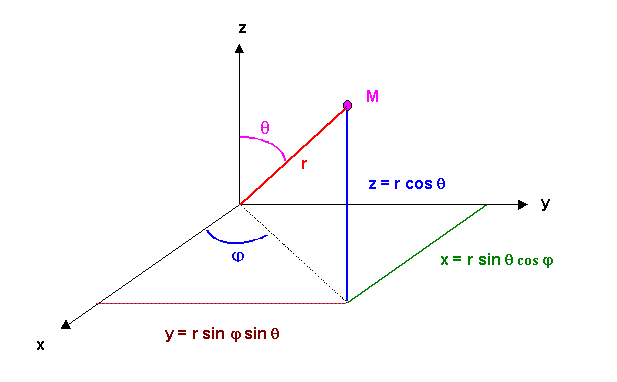
On peut résoudre l'équation différentielle dans ces coordonnées sphériques, on montre que les variables r, j et q sont séparables. La fonction d'onde Y est alors le produit de trois fonctions dépendant chacune uniquement d'une de ces trois variables.
Y (r, j , q ) = R ( r ) * q ( q ) * F ( j )
La fonction R ( r ) est appelée partie radiale, le produit des fonctions q ( q ) * F ( j ) est appelé partie angulaire.
La résolution de l'équation de Schrödinger, amène naturellement les trois nombres quantiques n, l et m comme nous l'avions précédemment signalé.
Expressions des premières fonctions d'onde pour l'atome d'Hydrogène :
Orbitale 1 s
n = 1, l = 0 , m = 0
Y 1s (r, j , q ) = 1/Ö p (Z/a0)3/2 exp (- Z r / a0)
Orbitale 2 s
n = 2, l = 0 , m = 0
Y 2s (r, j , q ) = 1/4Ö 2p (Z/a0)3/2 exp ( 2 - ( Z r / a0))
Orbitale 2 pz
n = 2, l = 1 , m = 0
Y 2pz (r, j , q ) = 1/4Ö 2p (Z/a0)3/2 (Z r / a0) exp ( - Z r / 2a0) cos q
Orbitale 2 px
n = 2, l = 1 , m = 1
Y 2px (r, j , q ) = 1/4Ö 2p (Z/a0)3/2 (Z r / a0) exp ( - Z r / 2a0) sin q cos j
Orbitale 2 py
n = 2, l = 1 , m = -1
Y 2py (r, j , q ) = 1/4Ö 2p (Z/a0)3/2 (Z r / a0) exp ( - Z r / 2a0) sin q sin j
Remarquons que les fonctions 1s et 2s ne font apparaître que la variable r, cela signifie pratiquement que leur partie angulaire est constante. En d'autre terme la fonction Y ne dépend que de la valeur de r, pour une même distance au noyau cette fonction aura la même valeur quel que soit la direction.
Si la fonction Y n'a pas de signification physique par elle-même, rappelons que son carré représente la probabilité de présence de l'électron. Si Y est constant, il en sera de même pour son carré. La probabilité de trouver l'électron à une certaine distance du noyau est donc constante quelle que soit la direction choisie. Ce type d'orbitale présentent donc une symétrie sphérique. Cela est général pour toute les orbitales de type s pour lesquelles la valeur de l est nulle.
On représente conventionnellement ce type d'orbitale par une sphère centrée sur le noyau.
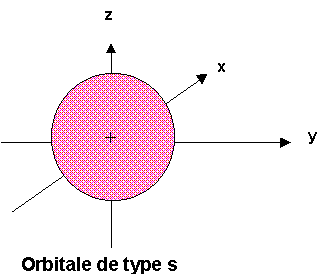
Cette sphère ne représente en réalité que la symétrie de l'orbitale, la taille qu'on lui assignera dépendra de la probabilité de présence de l'électron choisie.
Cette probabilité de présence de l'électron dans une sphère de rayon donné est calculable à partir de l'équation de Y et de la relation dP/dV = Y 2 soit P = ò ò ò Y 2 dV
Nous ne donnerons ici que les résultats numériques :
R (Å) |
0,26 |
1,06 |
1,67 |
3 |
¥ |
P |
0,08 |
0,76 |
0,95 |
0,999 |
1 |
La probabilité de trouver l'électron n'est rigoureusement égale à un que pour une sphère de rayon infini. Mais on constate que la probabilité devient rapidement très proche de 1 dès que r prend une valeur de l'ordre de grandeur de l'Angström (Å). Cela montre qu'il est possible avec une très bonne approximation de considérer les atomes comme des objet de dimension finit et qu'il est donc possible de leur attribuer un rayon.
Le mot orbitale désigne à la fois la fonction d'onde Y et le volume correspondant à une certaine probabilité de présence de l'électron fixée arbitrairement (95 % par exemple), dans le cas d'une orbitale s ce volume est sphérique. Il n'en va pas de même pour les orbitales pour lesquelles l n'est pas nul de type p , d, f etc. La fonction d'onde dépend alors des grandeurs angulaires q et j . Dans ce cas, la probabilité de présence prend des valeurs différentes en fonction de la direction. La symétrie de ces orbitales n'est donc plus sphérique. Elles posséderont donc une certaine forme géométrique qui leur sera propre. Pour représenter cette forme géométrique on utilise généralement le carré de leur partie angulaire. On obtient ainsi une enveloppe généralement en forme de lobe qui correspond à une probabilité de présence de l'électron préalablement fixée (95 % par exemple).
On représente les orbitales atomiques en faisant figurer le signe de la fonction d'onde.
Les trois orbitales p présentent une symétrie de révolution autour des trois axes x, y et z., leur forme géométrique est la suivante :
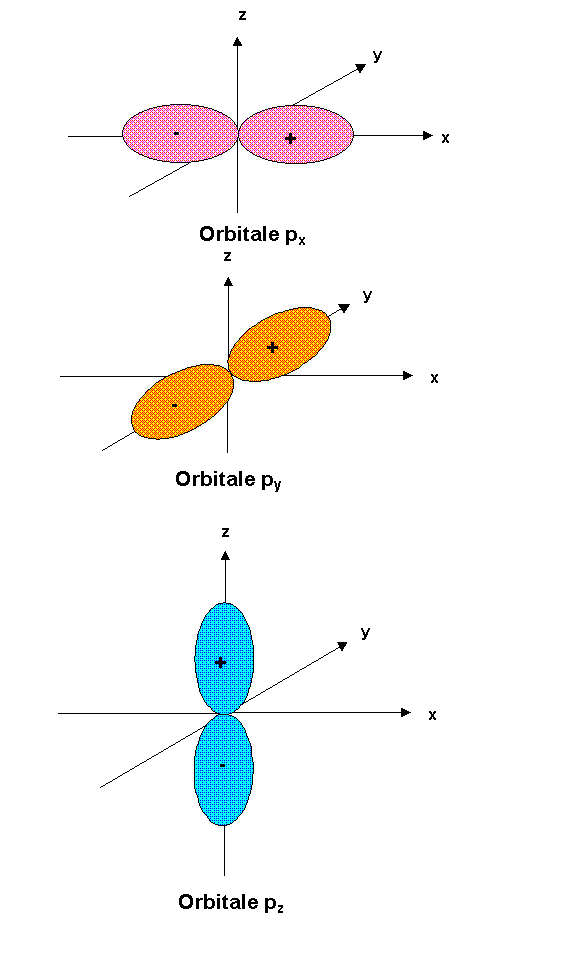
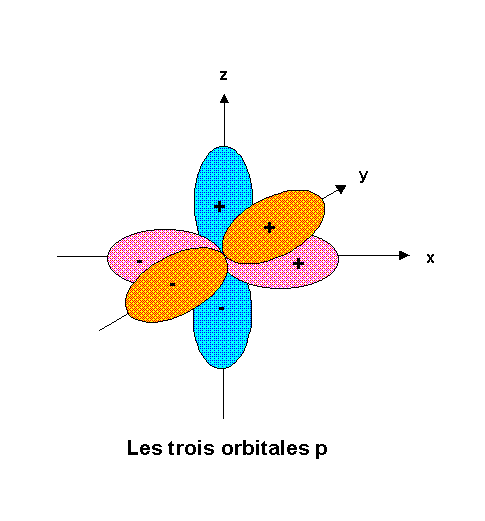
On peut de la même manière définir une forme géométrique pour les 5 orbitales d.
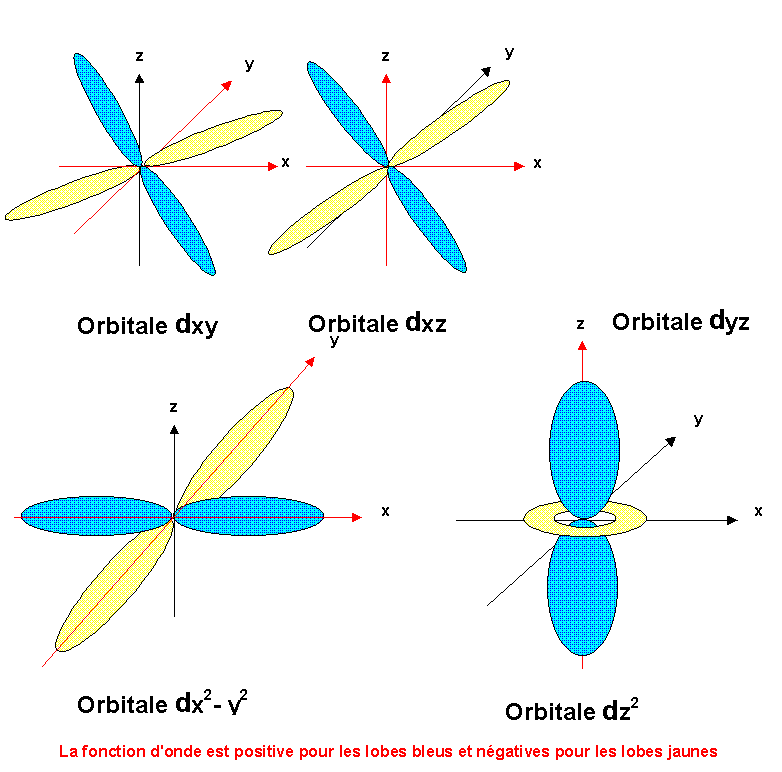
On peut distinguer deux types d'orbitales d, les orbitales dxy, dyz et dxz dont les lobes pointent dans des directions correspondant aux médiatrices des axes principaux et les orbitales dx2-y2 et dz2 dont les lobes pointent dans la direction des axes principaux.
Pour les atomes polyélectroniques (autre que H ou les hydrogénoïdes) on admettra que les résultats obtenus pour l'Hydrogène restent sensiblement valables.