Exercice 1 :

1. Equation de Schrödingerf = A sin ( 2 p x / l) cos ( 2 p n t )

   Le terme A cos ( 2 p n t ) ne dépend pas de x et peut donc être considéré comme constant, posons : A cos ( 2 p n t ) = B

   f = B sin ( 2 p x / l)

   f' = [ 2 p B / l ] cos ( 2 p x / l)

   f'' = [ - 4 p² B / l² ] sin ( 2 p x / l)

   f'' = [ - 4 p² / l² ] B sin ( 2 p x / l)

   f'' = [ - 4 p² / l² ] f

   Formule de de Broglie

   l = h / p

   l² = h² / p²

   p = m v

   p² = m² v²

   E_C = 1/2 m v²

   m E_C = 1/2 m² v²

   2 m E_C = m² v² = p²

   1/ l² = p² / h² = 2 m E_C / h²

   f'' = - 4 p² / l² f = [ - 8 p² m E_C / h²] f = [ - 8 p² m / h²] E_C f

   E_T = E_C + E_P

   E_C = E_T - E_P = E - V

   f'' = [ - 8 p² m / h²] (E - V) f

   f'' + [ 8 p² m / h²] (E - V) f = 0

   Dans ce problème "a une seule dimension", on retrouve bien l'équation de Schrödinger, en mécanique quantique, sa généralisation à trois dimensions est postulée.

2. Valeurs propres de l'énergie :

Corde vibrante

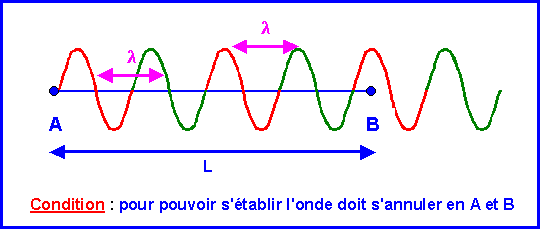
Supposons une corde vibrante tendue entre deux points A et B distant d'une longueur L.

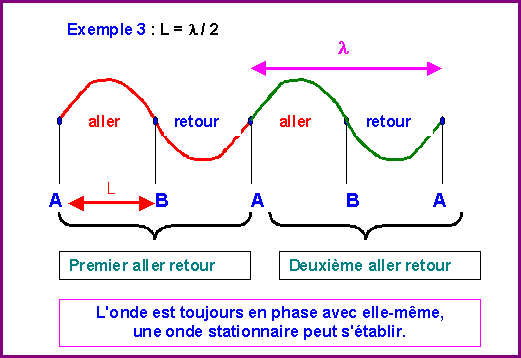
Pour qu'une onde stable stationnaire puisse s'établir, il faut que celle-ci puisse faire des aller-retour entre les deux points sans interférer avec elle-même. Cela introduit une contrainte, la longueur d'onde ne peut pas être quelconques mais ne peut prendre que certaines valeurs bien précise, il y donc une quantification de la fonction d'onde.

La condition est que l'onde s'annule aux deux extrémités A et B.

Pour cela il faut que la longueur entre A et B contienne un nombre entier de fois la demi-longueur d'onde

L = k l / 2 avec k entier

Prenons des exemples :

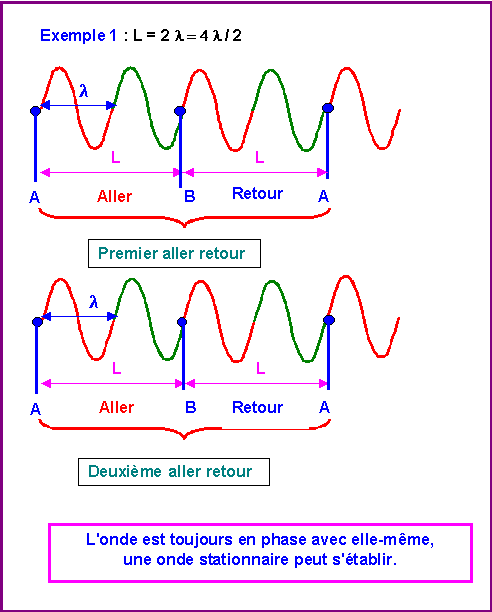
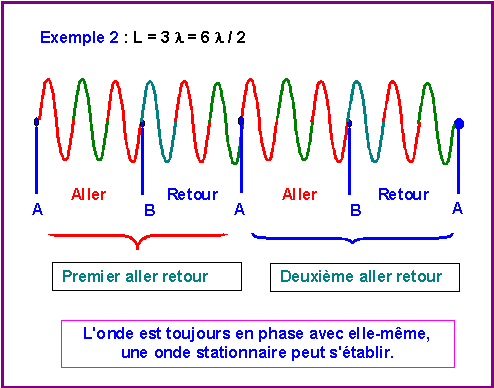
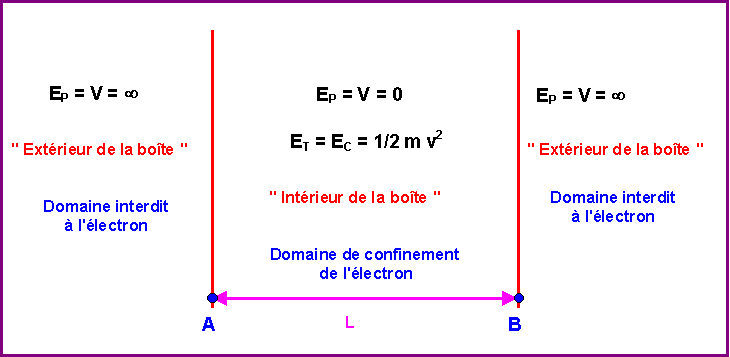
Par analogie, pour un électron dans une "boite à une dimension" :

A l'intérieur de la boîte l'énergie potentielle est nulle et l'électron possède une énergie purement cinétique.

A l'extérieur de la boîte l'énergie potentielle est infinie et l'électron ne peut donc sortir de la boîte à l'intérieur de laquelle il est confiné.

Calcul de l'énergie :

E_C = 1/2 m v²

m E_C = 1/2 m² v²

2 m E_C = m² v² = p²

1 / l² = p² / h² = 2 m E_C / h²

L = k l / 2 (avec k entier)

1 / l = k / 2 L

1 / l² = k ² / 4 L²

1 / l² = 2 m E_C / h² = k ² / 4 L²

2 m E_C / h² = k ² / 4 L²

E_C = E_T = [1/ 8 m h² ] { k² / L² }

L'énergie de l'électron à l'intérieur de la boîte est quantifiée et ne peut donc prendre que certaines valeurs bien précises fonction d'un nombre entier k appelé nombre quantique principal. Elle dépend également de la longueur L de la boîte, et est inversement proportionnelle au carré de celle-ci..

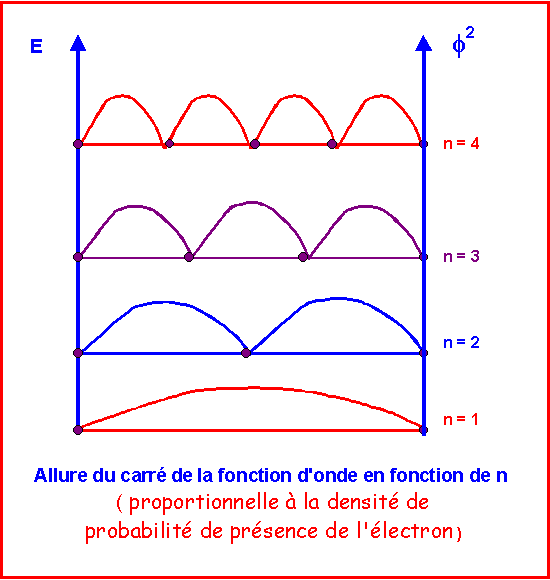
3) Représentations graphiques

E_C = E_T = [ 1/ ( 8 m h² ) ] { k² / L² } = [ 1/ ( 8 m h² L² ) ] k²

On pose C = [ 1/ ( 8 m h² L² ) ] pour alléger l'écriture

Soit : E = C k²

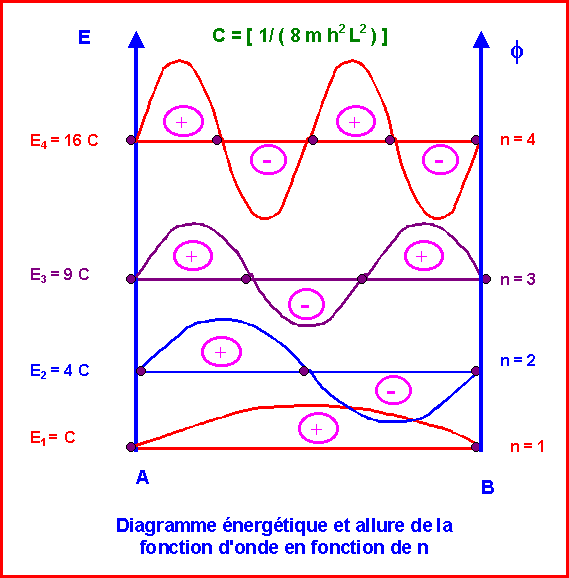
Un nœud est un point pour lequel la fonction d'onde s'annule.

Le carré de la fonction d'onde est proportionnel à la densité de probabilité de présence de l'électron en un point.

La probabilité de présence est nulle aux nœuds et maximale entre les nœuds.

Retour aux énoncés